選択肢4が正解です。 次の身長のDataFrameで確認します。 df = pd.DataFrame( {'身長': [155, 158, 160, 163, 165, 166, 170, 175, 178, 200]}) ▶︎ 【選択肢1】 Plotly Expressのbox関数による確認。 正しい説明です。 px.box(df, y='身長') ▶︎ 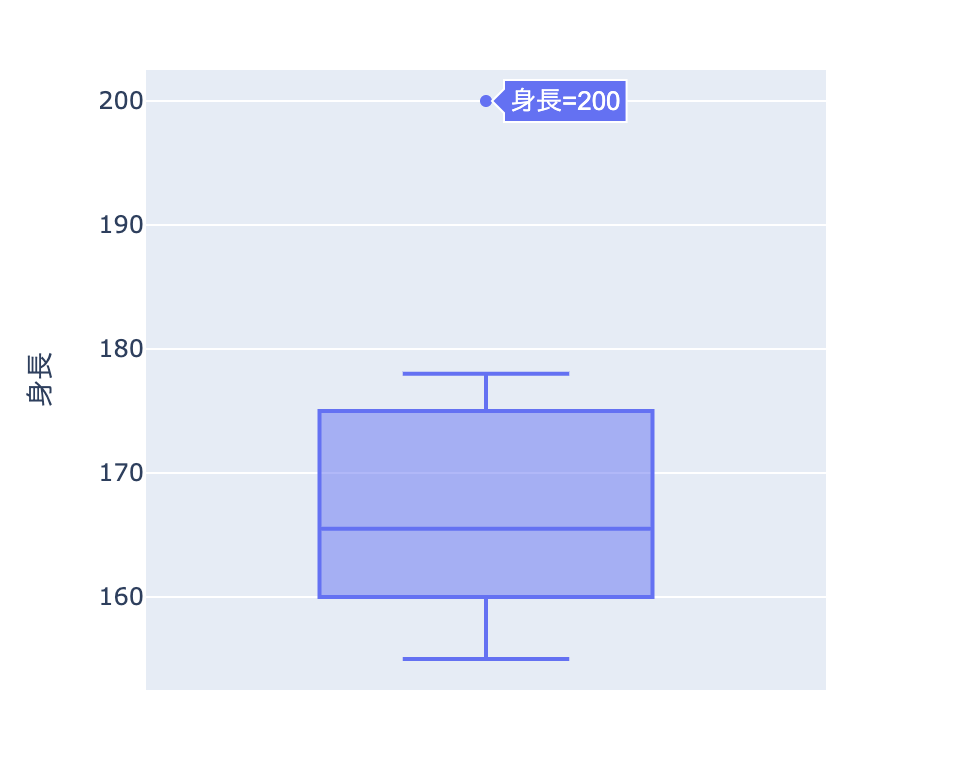Plotly Expressのグラフは、要素にマウスオーバーすると値を確認できます。 上の箱ひげ図は、一番上の外れ値にマウスオーバーしており、身長=200が外れ値であることが確認できます。 箱ひげ図の外れ値は、四分位範囲（25%〜75%）から1.5倍以上離れた値が外れ値になります。 【選択肢2】 pandasのquantileメソッドによる確認。 正しい説明です。 quantileメソッドは分位点の値を特定できます。 例えば、95%〜100%の範囲にある値を外れ値と仮定して、quantileメソッドに「0.95」の引数を指定します。引数は百分率（%）の値ではなく、小数で指定します。 df.quantile(0.95) ▶︎ 身長 190.1 全体の95%の位置にある値が、190.1であることが分かります。これを超える値が外れ値になります。 このDataFrameはデータ数が少ないため、目視で「200」が外れ値であることを確認できますが、通常はqueryメソッドなどでレコードを特定します。 df.query('身長 > 190.1') ▶︎ 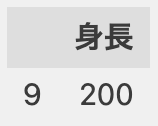必要に応じて該当の行を削除することで、外れ値を除外します。 【選択肢3】 正規分布と2σ範囲による確認。 正しい説明です。 2σは「標準偏差の2倍」という意味です。データが正規分布の場合、標準偏差の2倍を超える範囲は、両端の約2.5%になります。この2.5%の範囲にある値を外れ値と考えて、値を特定します。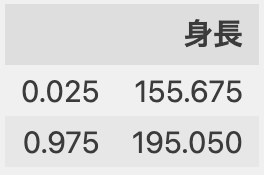 df.quantile(q=[0.025, 0.975]) ▶︎ 2.5%の位置にある値が155.675、97.5%の位置にある値が195.050と分かりました。これを超える両端の値が外れ値になります。 【選択肢4】 pandasのcut関数で%を指定して確認。 誤った説明です。 cut関数は値をカテゴリに変換する関数です。 例えば身長の値を160と170で分ける場合、以下の記述になります。 pd.cut(df['身長'], bins=[0, 160, 170, 201], right=False) ▶︎ 0 [0, 160) 1 [0, 160) 2 [160, 170) 3 [160, 170) 4 [160, 170) 5 [160, 170) 6 [170, 201) 7 [170, 201) 8 [170, 201) 9 [170, 201) この場合、各値は以下のカテゴリに属することがわかります。 インデックス0〜1 ▶︎ [0, 160) ＊0以上、160未満 インデックス2〜5 ▶︎ [160, 170) ＊160以上、170未満 インデックス6〜9 ▶︎ [170, 201) ＊170以上、201未満 cut関数のbins引数は割合を指定するのではなく、データの値を直接指定します。身長であれば160や170などの値を指定してカテゴリを分けます。quantileメソッドの0.025（2.5%）のように、割合を指定することはできません。 選択肢2のquantileメソッドで外れ値の閾値を特定できているのであれば、cut関数でも閾値を指定して外れ値を特定することができます。 pd.cut(df['身長'], bins=[0, 155.675, 195.050, 201], right=False) ▶︎ 0 [0.0, 155.675) 1 [155.675, 195.05) 2 [155.675, 195.05) 3 [155.675, 195.05) 4 [155.675, 195.05) 5 [155.675, 195.05) 6 [155.675, 195.05) 7 [155.675, 195.05) 8 [155.675, 195.05) 9 [195.05, 201.0) 両端の2.5%を外れ値とした場合、インデックス0とインデックス9が外れ値のカテゴリに属することが分かります。 （公式書籍 p.181-185）