データ分析・初級問題チェック
問題 12 /40
統計の代表値に関する説明で、誤っているものはどれか。
選択 1
算術平均は、複数の値を足し合わせて、値の数で割って求める。
選択 2
平均は算術平均だけではなく、相乗平均や調和平均などもある。
選択 3
中央値は、データを小さい順に並べて、ちょうど真ん中に来る値を指す。データの個数が偶数の場合は、中間に位置する2つのデータの小さいほうを中央値とする。
選択 4
最頻値とは、最も頻繁に出現するデータである。
解説
選択肢3が正解です。
中央値を求める際、データの個数が偶数だった場合は、中央に位置する2つのデータの平均を中央値とします。
平均には算術平均(相加平均)、相乗平均、調和平均があり、計算式は以下となります。
【算術平均】
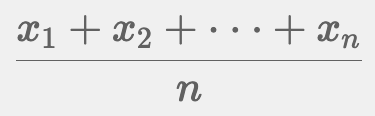 一般的な平均です。
【相乗平均】
一般的な平均です。
【相乗平均】
 データがn個あったら、n個のデータを掛け合わせて、そのn乗根を取ります。例えば「2」と「8」というデータがあった場合、「2x8=16」となり、16の2乗根を取るため「4」となります。
相乗平均は増加率や成長率の平均を求める場合などに利用します。国民の平均年収など、正規分布しないデータも、算術平均よりも相乗平均のほうが実際の感覚に近い数値を出せることがあります。
【調和平均】
データがn個あったら、n個のデータを掛け合わせて、そのn乗根を取ります。例えば「2」と「8」というデータがあった場合、「2x8=16」となり、16の2乗根を取るため「4」となります。
相乗平均は増加率や成長率の平均を求める場合などに利用します。国民の平均年収など、正規分布しないデータも、算術平均よりも相乗平均のほうが実際の感覚に近い数値を出せることがあります。
【調和平均】
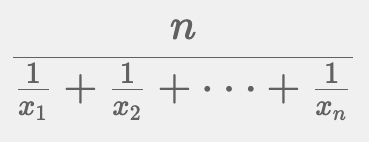 速度の平均や、電気回路の電圧を求める場合などに利用します。
例えば、10kmを時速50km/hで進んだ後、さらに10kmを時速100km/hで進んだときの平均速度を考えます。
速度の平均や、電気回路の電圧を求める場合などに利用します。
例えば、10kmを時速50km/hで進んだ後、さらに10kmを時速100km/hで進んだときの平均速度を考えます。
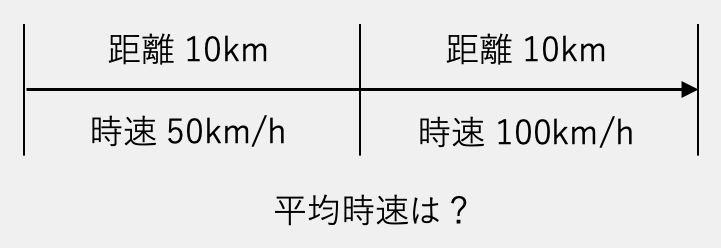 次の図は、距離・速さ・時間を求める「きはじ」の公式です。例えば、時間を求める場合は「じ」を隠して、「距離(き) ÷ 速さ(は)」で求めます。
次の図は、距離・速さ・時間を求める「きはじ」の公式です。例えば、時間を求める場合は「じ」を隠して、「距離(き) ÷ 速さ(は)」で求めます。
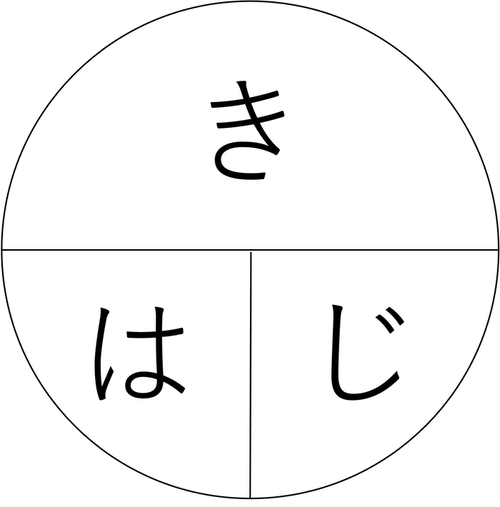 「きはじ」の公式で合計時間を求めると、「0.2 (10km ÷ 50km/h) + 0.1 (10km ÷ 100km/h) = 0.3時間」となります。
また、例題の平均速度を一般的な算術平均で求めると、「150 (50km/h + 100km/h ) ÷ 2 = 75km/h」 となります。
この「75km/h」が正しいのか確認するために、距離の合計「20km」と計算して合計時間を求めます。
平均速度75km/hで20km進んだときの時間は、「20km ÷ 75km/h = 0.26...時間」となり、先に計算した実際の所要時間「0.3時間」と一致しません。
そこで調和平均を使って平均速度を求めます。
調和平均の式に、今回の時速を入れて平均速度を求めると次の式になり、結果は「66.6...km/h」となります。
「きはじ」の公式で合計時間を求めると、「0.2 (10km ÷ 50km/h) + 0.1 (10km ÷ 100km/h) = 0.3時間」となります。
また、例題の平均速度を一般的な算術平均で求めると、「150 (50km/h + 100km/h ) ÷ 2 = 75km/h」 となります。
この「75km/h」が正しいのか確認するために、距離の合計「20km」と計算して合計時間を求めます。
平均速度75km/hで20km進んだときの時間は、「20km ÷ 75km/h = 0.26...時間」となり、先に計算した実際の所要時間「0.3時間」と一致しません。
そこで調和平均を使って平均速度を求めます。
調和平均の式に、今回の時速を入れて平均速度を求めると次の式になり、結果は「66.6...km/h」となります。
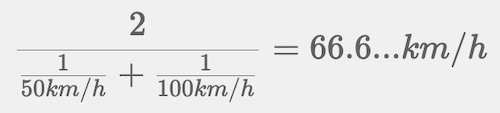 66.6km/hで20km進んだときの時間は「20km ÷ 66.6km/h = 0.3...時間」となり、実際の所要時間と近似します。
調和平均は、平均を求める対象が同じ数字の分子で算出された場合に利用します。今回の例題では、最初にそれぞれの速度を求めた際に、分子となる2つの距離が10kmと10kmで同じだったため、算術平均ではなく調和平均が適切でした。距離が10kmと20kmのように異なっている場合は算術平均が適しています。
機械学習の分類モデルの評価で用いるF値は、適合率と再現率の調和平均で計算します。適合率も再現率も、どちらも分子が「TP(正例と予測して実際に正例)」であるため、算術平均ではなく調和平均が適しています。F値の詳細は上級問題38で解説します。
なお、大小の関係で見ると「算術平均 ≧ 相乗平均 ≧ 調和平均」となります。
(公式書籍 p.76-77)
66.6km/hで20km進んだときの時間は「20km ÷ 66.6km/h = 0.3...時間」となり、実際の所要時間と近似します。
調和平均は、平均を求める対象が同じ数字の分子で算出された場合に利用します。今回の例題では、最初にそれぞれの速度を求めた際に、分子となる2つの距離が10kmと10kmで同じだったため、算術平均ではなく調和平均が適切でした。距離が10kmと20kmのように異なっている場合は算術平均が適しています。
機械学習の分類モデルの評価で用いるF値は、適合率と再現率の調和平均で計算します。適合率も再現率も、どちらも分子が「TP(正例と予測して実際に正例)」であるため、算術平均ではなく調和平均が適しています。F値の詳細は上級問題38で解説します。
なお、大小の関係で見ると「算術平均 ≧ 相乗平均 ≧ 調和平均」となります。
(公式書籍 p.76-77)
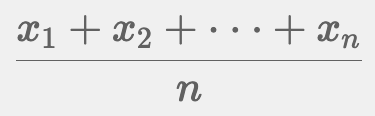 一般的な平均です。
【相乗平均】
一般的な平均です。
【相乗平均】
 データがn個あったら、n個のデータを掛け合わせて、そのn乗根を取ります。例えば「2」と「8」というデータがあった場合、「2x8=16」となり、16の2乗根を取るため「4」となります。
相乗平均は増加率や成長率の平均を求める場合などに利用します。国民の平均年収など、正規分布しないデータも、算術平均よりも相乗平均のほうが実際の感覚に近い数値を出せることがあります。
【調和平均】
データがn個あったら、n個のデータを掛け合わせて、そのn乗根を取ります。例えば「2」と「8」というデータがあった場合、「2x8=16」となり、16の2乗根を取るため「4」となります。
相乗平均は増加率や成長率の平均を求める場合などに利用します。国民の平均年収など、正規分布しないデータも、算術平均よりも相乗平均のほうが実際の感覚に近い数値を出せることがあります。
【調和平均】
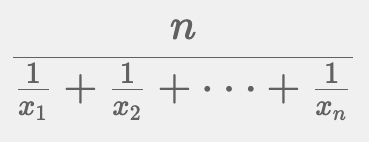 速度の平均や、電気回路の電圧を求める場合などに利用します。
例えば、10kmを時速50km/hで進んだ後、さらに10kmを時速100km/hで進んだときの平均速度を考えます。
速度の平均や、電気回路の電圧を求める場合などに利用します。
例えば、10kmを時速50km/hで進んだ後、さらに10kmを時速100km/hで進んだときの平均速度を考えます。

 「きはじ」の公式で合計時間を求めると、「0.2 (10km ÷ 50km/h) + 0.1 (10km ÷ 100km/h) = 0.3時間」となります。
また、例題の平均速度を一般的な算術平均で求めると、「150 (50km/h + 100km/h ) ÷ 2 = 75km/h」 となります。
この「75km/h」が正しいのか確認するために、距離の合計「20km」と計算して合計時間を求めます。
平均速度75km/hで20km進んだときの時間は、「20km ÷ 75km/h = 0.26...時間」となり、先に計算した実際の所要時間「0.3時間」と一致しません。
そこで調和平均を使って平均速度を求めます。
調和平均の式に、今回の時速を入れて平均速度を求めると次の式になり、結果は「66.6...km/h」となります。
「きはじ」の公式で合計時間を求めると、「0.2 (10km ÷ 50km/h) + 0.1 (10km ÷ 100km/h) = 0.3時間」となります。
また、例題の平均速度を一般的な算術平均で求めると、「150 (50km/h + 100km/h ) ÷ 2 = 75km/h」 となります。
この「75km/h」が正しいのか確認するために、距離の合計「20km」と計算して合計時間を求めます。
平均速度75km/hで20km進んだときの時間は、「20km ÷ 75km/h = 0.26...時間」となり、先に計算した実際の所要時間「0.3時間」と一致しません。
そこで調和平均を使って平均速度を求めます。
調和平均の式に、今回の時速を入れて平均速度を求めると次の式になり、結果は「66.6...km/h」となります。
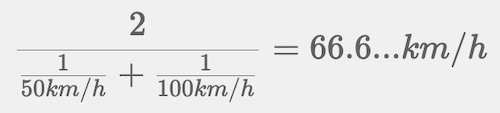 66.6km/hで20km進んだときの時間は「20km ÷ 66.6km/h = 0.3...時間」となり、実際の所要時間と近似します。
調和平均は、平均を求める対象が同じ数字の分子で算出された場合に利用します。今回の例題では、最初にそれぞれの速度を求めた際に、分子となる2つの距離が10kmと10kmで同じだったため、算術平均ではなく調和平均が適切でした。距離が10kmと20kmのように異なっている場合は算術平均が適しています。
機械学習の分類モデルの評価で用いるF値は、適合率と再現率の調和平均で計算します。適合率も再現率も、どちらも分子が「TP(正例と予測して実際に正例)」であるため、算術平均ではなく調和平均が適しています。F値の詳細は上級問題38で解説します。
なお、大小の関係で見ると「算術平均 ≧ 相乗平均 ≧ 調和平均」となります。
(公式書籍 p.76-77)
66.6km/hで20km進んだときの時間は「20km ÷ 66.6km/h = 0.3...時間」となり、実際の所要時間と近似します。
調和平均は、平均を求める対象が同じ数字の分子で算出された場合に利用します。今回の例題では、最初にそれぞれの速度を求めた際に、分子となる2つの距離が10kmと10kmで同じだったため、算術平均ではなく調和平均が適切でした。距離が10kmと20kmのように異なっている場合は算術平均が適しています。
機械学習の分類モデルの評価で用いるF値は、適合率と再現率の調和平均で計算します。適合率も再現率も、どちらも分子が「TP(正例と予測して実際に正例)」であるため、算術平均ではなく調和平均が適しています。F値の詳細は上級問題38で解説します。
なお、大小の関係で見ると「算術平均 ≧ 相乗平均 ≧ 調和平均」となります。
(公式書籍 p.76-77)