データ分析・初級問題チェック
問題 8 /40
数学に関する説明で、誤っているものはどれか。
選択 1
次の式は、「x=0」と「x=1」を解に持つ2次方程式である。
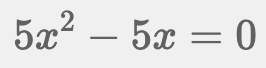
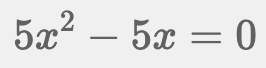
選択 2
直径が1の円の円周は3.14...で、これが円周率πである。
選択 3
ネイピア数eは2.71...で、常用対数の底である。
選択 4
足し算を繰り返す記号はΣ(シグマ)を使い、すべてを掛け合わせる記号はΠ(パイ)を使う。
解説
選択肢3が正解です。
【選択肢1】
次の式は、「x=0」と「x=1」を解に持つ2次方程式である。
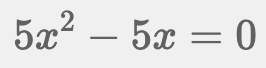 正しい説明です。
この式を展開すると、「5x(x-1)=0」になります。5xと(x-1)の間には、掛け算の記号が隠れています。掛けた結果を0にするには、5xか(x-1)のどちらかを0にする必要があります。そのため、x=0(5xのxに0を代入する)、もしくはx=1(x-1のxに1を代入する)が解になります。
この式はxの2乗が最高の次数となるため2次方程式です。また、変数xの前の数字「5」は、係数と呼ばれます。
【選択肢2】
直径が1の円の円周は3.14...で、これが円周率πである。
正しい説明です。
【選択肢3】
ネイピア数eは2.71...で、常用対数の底である。
誤った説明です。
ネイピア数e(2.71...)は自然対数の底で、常用対数の底ではありません。常用対数の底は10です。
対数は指数を求めるための道具です。例えば次の式は、「2を底とした8の対数は3」という意味で、「2を何乗すると8になるか」の解が「3」となります。
正しい説明です。
この式を展開すると、「5x(x-1)=0」になります。5xと(x-1)の間には、掛け算の記号が隠れています。掛けた結果を0にするには、5xか(x-1)のどちらかを0にする必要があります。そのため、x=0(5xのxに0を代入する)、もしくはx=1(x-1のxに1を代入する)が解になります。
この式はxの2乗が最高の次数となるため2次方程式です。また、変数xの前の数字「5」は、係数と呼ばれます。
【選択肢2】
直径が1の円の円周は3.14...で、これが円周率πである。
正しい説明です。
【選択肢3】
ネイピア数eは2.71...で、常用対数の底である。
誤った説明です。
ネイピア数e(2.71...)は自然対数の底で、常用対数の底ではありません。常用対数の底は10です。
対数は指数を求めるための道具です。例えば次の式は、「2を底とした8の対数は3」という意味で、「2を何乗すると8になるか」の解が「3」となります。
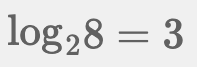 この式の底は2ですが、通常はネイピア数や10を底にして利用します。
対数はスケール変換で利用できます。例えば10万と1000万という数値があった場合、そのままの数では大きな差異がありますが、常用対数に変換すると5と7になるため、比べ易くなります(10万は10の5乗で、1000万は10の7乗です)。
対数は「天文学者の寿命を倍に延ばした」と言われています。計算機が無い時代に、大きい数の計算が楽になったからです。
【選択肢4】
足し算を繰り返す記号はΣ(シグマ)を使い、すべてを掛け合わせる記号はΠ(パイ)を使う。
正しい説明です。
Σ(シグマ)は足し算を繰り返します。次の式は、iに1から4まで順番に代入し、足し合わせます。解は「1+2+3+4=10」です。
この式の底は2ですが、通常はネイピア数や10を底にして利用します。
対数はスケール変換で利用できます。例えば10万と1000万という数値があった場合、そのままの数では大きな差異がありますが、常用対数に変換すると5と7になるため、比べ易くなります(10万は10の5乗で、1000万は10の7乗です)。
対数は「天文学者の寿命を倍に延ばした」と言われています。計算機が無い時代に、大きい数の計算が楽になったからです。
【選択肢4】
足し算を繰り返す記号はΣ(シグマ)を使い、すべてを掛け合わせる記号はΠ(パイ)を使う。
正しい説明です。
Σ(シグマ)は足し算を繰り返します。次の式は、iに1から4まで順番に代入し、足し合わせます。解は「1+2+3+4=10」です。
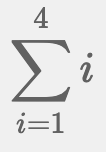 Π(パイ)は掛け合わせます。次の式は、iに1から4まで順番に代入し、掛け合わせます。解は「1×2×3×4=24」です。
Π(パイ)は掛け合わせます。次の式は、iに1から4まで順番に代入し、掛け合わせます。解は「1×2×3×4=24」です。
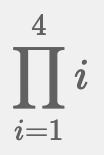 (公式書籍 p.53-54)
(公式書籍 p.53-54)
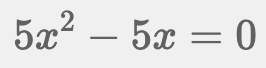 正しい説明です。
この式を展開すると、「5x(x-1)=0」になります。5xと(x-1)の間には、掛け算の記号が隠れています。掛けた結果を0にするには、5xか(x-1)のどちらかを0にする必要があります。そのため、x=0(5xのxに0を代入する)、もしくはx=1(x-1のxに1を代入する)が解になります。
この式はxの2乗が最高の次数となるため2次方程式です。また、変数xの前の数字「5」は、係数と呼ばれます。
【選択肢2】
直径が1の円の円周は3.14...で、これが円周率πである。
正しい説明です。
【選択肢3】
ネイピア数eは2.71...で、常用対数の底である。
誤った説明です。
ネイピア数e(2.71...)は自然対数の底で、常用対数の底ではありません。常用対数の底は10です。
対数は指数を求めるための道具です。例えば次の式は、「2を底とした8の対数は3」という意味で、「2を何乗すると8になるか」の解が「3」となります。
正しい説明です。
この式を展開すると、「5x(x-1)=0」になります。5xと(x-1)の間には、掛け算の記号が隠れています。掛けた結果を0にするには、5xか(x-1)のどちらかを0にする必要があります。そのため、x=0(5xのxに0を代入する)、もしくはx=1(x-1のxに1を代入する)が解になります。
この式はxの2乗が最高の次数となるため2次方程式です。また、変数xの前の数字「5」は、係数と呼ばれます。
【選択肢2】
直径が1の円の円周は3.14...で、これが円周率πである。
正しい説明です。
【選択肢3】
ネイピア数eは2.71...で、常用対数の底である。
誤った説明です。
ネイピア数e(2.71...)は自然対数の底で、常用対数の底ではありません。常用対数の底は10です。
対数は指数を求めるための道具です。例えば次の式は、「2を底とした8の対数は3」という意味で、「2を何乗すると8になるか」の解が「3」となります。
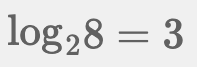 この式の底は2ですが、通常はネイピア数や10を底にして利用します。
対数はスケール変換で利用できます。例えば10万と1000万という数値があった場合、そのままの数では大きな差異がありますが、常用対数に変換すると5と7になるため、比べ易くなります(10万は10の5乗で、1000万は10の7乗です)。
対数は「天文学者の寿命を倍に延ばした」と言われています。計算機が無い時代に、大きい数の計算が楽になったからです。
【選択肢4】
足し算を繰り返す記号はΣ(シグマ)を使い、すべてを掛け合わせる記号はΠ(パイ)を使う。
正しい説明です。
Σ(シグマ)は足し算を繰り返します。次の式は、iに1から4まで順番に代入し、足し合わせます。解は「1+2+3+4=10」です。
この式の底は2ですが、通常はネイピア数や10を底にして利用します。
対数はスケール変換で利用できます。例えば10万と1000万という数値があった場合、そのままの数では大きな差異がありますが、常用対数に変換すると5と7になるため、比べ易くなります(10万は10の5乗で、1000万は10の7乗です)。
対数は「天文学者の寿命を倍に延ばした」と言われています。計算機が無い時代に、大きい数の計算が楽になったからです。
【選択肢4】
足し算を繰り返す記号はΣ(シグマ)を使い、すべてを掛け合わせる記号はΠ(パイ)を使う。
正しい説明です。
Σ(シグマ)は足し算を繰り返します。次の式は、iに1から4まで順番に代入し、足し合わせます。解は「1+2+3+4=10」です。
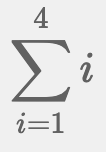 Π(パイ)は掛け合わせます。次の式は、iに1から4まで順番に代入し、掛け合わせます。解は「1×2×3×4=24」です。
Π(パイ)は掛け合わせます。次の式は、iに1から4まで順番に代入し、掛け合わせます。解は「1×2×3×4=24」です。
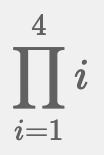 (公式書籍 p.53-54)
(公式書籍 p.53-54)