データ分析・中級問題チェック
問題 8 /40
三角関数に関する説明で、誤っているものはどれか。
選択 1
sinを正弦、cosを余弦、tanを正接と呼ぶ。
選択 2
sinθ、cosθ、tanθは比である。(θ=シータ)
選択 3
cos0°の三角比は0である。(0=ゼロ)
選択 4
弧度法の単位(ラジアン)は、1周を2πとする。
解説
選択肢3が正解です。
【選択肢1、2】
正しい説明です。
sinを正弦、cosを余弦、tanを正接と呼び、sinθ、cosθ、tanθは比を表します。
【選択肢3】
cos0°の三角比は0ではなく1です。
0°から90°までの三角比は以下となります。
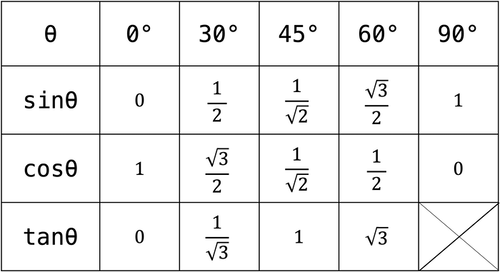 三角比は半径1の単位円で考えると理解しやすいです。
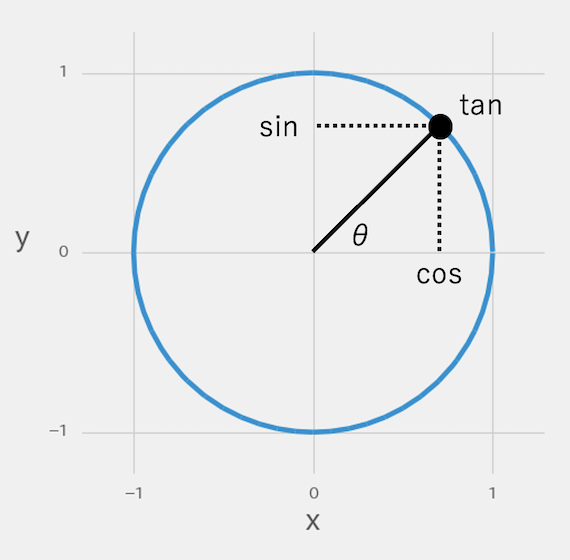
まず、x軸の値がcos、y軸の値がsin、傾きの値がtanの三角比と覚えます。
また、原点(0,0)から円周上に対して引いた直線と、x軸との間にできた角度をθと考えます。
三角比は半径1の単位円で考えると理解しやすいです。
まず、x軸の値がcos、y軸の値がsin、傾きの値がtanの三角比と覚えます。
また、原点(0,0)から円周上に対して引いた直線と、x軸との間にできた角度をθと考えます。
 以下は例です。
■ sin30°
以下は例です。
■ sin30°
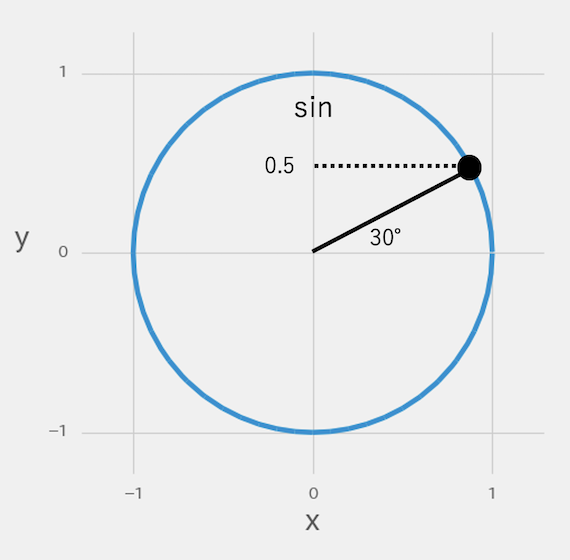 30°の直線でできた円周上の黒丸は、y軸に点線を引くと1の半分の位置に来るため、sin30°の三角比は0.5、つまり2分の1になります。
■ cos60°
30°の直線でできた円周上の黒丸は、y軸に点線を引くと1の半分の位置に来るため、sin30°の三角比は0.5、つまり2分の1になります。
■ cos60°
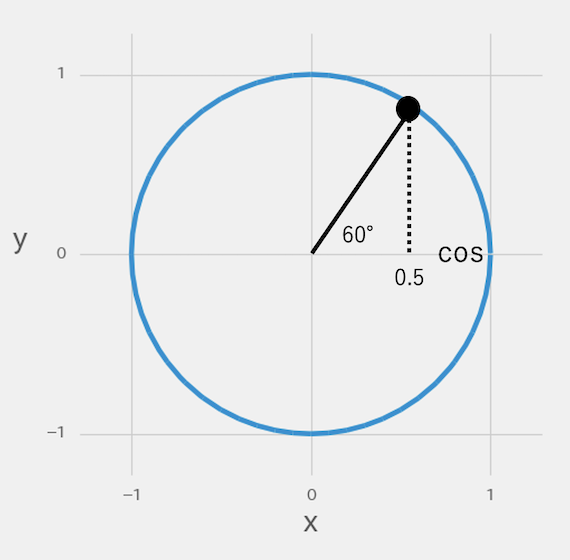 60°の直線でできた円周上の黒丸は、x軸に点線を引くと1の半分の位置に来るため、cos60°の三角比は0.5、つまり2分の1になります。
■ tan45°
60°の直線でできた円周上の黒丸は、x軸に点線を引くと1の半分の位置に来るため、cos60°の三角比は0.5、つまり2分の1になります。
■ tan45°
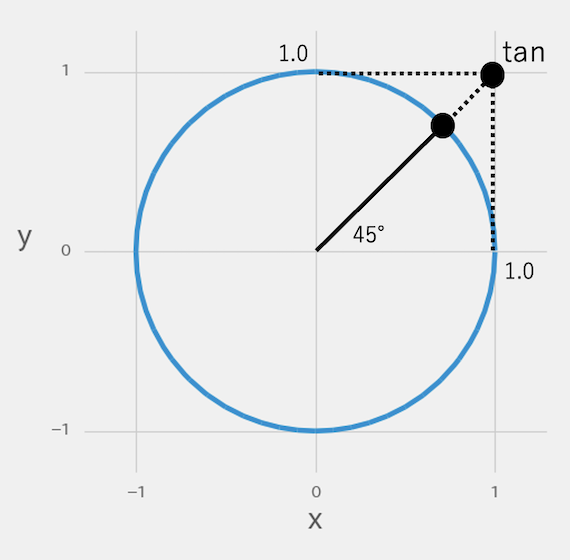 tanは傾きで考えます。45°の直線でできた円周上の黒丸は、延長するとx=1、y=1の座標で交わります。yの距離をxの距離で割って傾きを求めると1になるため、tan45°の三角比は1になります。
tan90°は三角比がありませんが、これも単位円で考えると理解できます。90°は垂線となり傾きがないため、三角比もありません。
こうして問題文のcos0°を考えると、0°の直線でできた円周上の黒丸はx軸上にあるため、x軸の値は1となり、cos0°の三角比も1となります。
【選択肢4】
円の一周の角度は0°から360°ですが、この1周を2πとして考えるのが弧度法です。直径1の円の円周がπ(3.14)で、先に紹介した半径1・直径2の単位円の円周がちょうど2πになります。
弧度法の単位はラジアンです。例えば360°は2πラジアン(3.14×2)、180°はπラジアン(3.14)、90°はπ/2ラジアン(3.14÷2)となります。
Numpyのsin関数などの引数もラジアンで指定します。sin関数の引数を-πからπ(-3.14から3.14)で指定してプロットすると、次の周期グラフになります。
tanは傾きで考えます。45°の直線でできた円周上の黒丸は、延長するとx=1、y=1の座標で交わります。yの距離をxの距離で割って傾きを求めると1になるため、tan45°の三角比は1になります。
tan90°は三角比がありませんが、これも単位円で考えると理解できます。90°は垂線となり傾きがないため、三角比もありません。
こうして問題文のcos0°を考えると、0°の直線でできた円周上の黒丸はx軸上にあるため、x軸の値は1となり、cos0°の三角比も1となります。
【選択肢4】
円の一周の角度は0°から360°ですが、この1周を2πとして考えるのが弧度法です。直径1の円の円周がπ(3.14)で、先に紹介した半径1・直径2の単位円の円周がちょうど2πになります。
弧度法の単位はラジアンです。例えば360°は2πラジアン(3.14×2)、180°はπラジアン(3.14)、90°はπ/2ラジアン(3.14÷2)となります。
Numpyのsin関数などの引数もラジアンで指定します。sin関数の引数を-πからπ(-3.14から3.14)で指定してプロットすると、次の周期グラフになります。
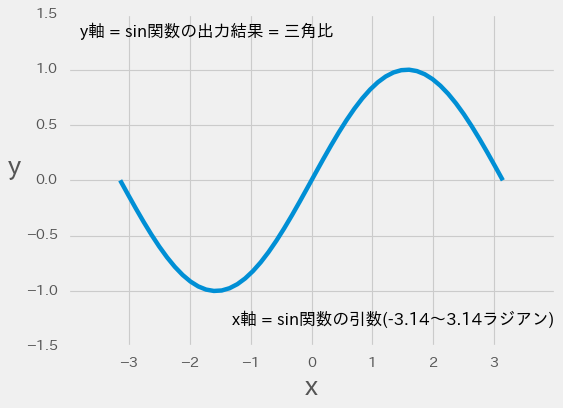 これも単位円で考えると理解しやすいです。上の周期グラフの場合、単位円の右端(0°)から、右回りに一周したときのy軸(sin)の値の動きが、周期グラフのy軸の値と一致します。
(公式書籍 p.59-60)
これも単位円で考えると理解しやすいです。上の周期グラフの場合、単位円の右端(0°)から、右回りに一周したときのy軸(sin)の値の動きが、周期グラフのy軸の値と一致します。
(公式書籍 p.59-60)





