データ分析・上級問題チェック
問題 10 /40
ベクトルに関する説明で、誤っているものはどれか。
選択 1
コサイン類似度は、-2から2の間の値を取る。
選択 2
機械学習の自然言語処理で、ベクトル化した単語同士の関係性を表す際に、コサイン類似度を利用する。
選択 3
線形変換後のベクトルが回転せず、拡大・縮小のみで表現できる場合のベクトルを固有ベクトル、その長さの比を固有値と呼ぶ。
選択 4
固有値・固有ベクトルは、教師なし学習の主成分分析で次元を削減するときに利用される。
解説
選択肢1が正解です。
コサイン類似度は、-1から1の間の値を取ります。
【コサイン類似度】
コサイン類似度とは、2つのベクトルの相関を、2つのベクトルの角度(cosθの三角比)で表したものです。
0°〜180°のcosθの三角比は、0°=1、45°=0.71、90°=0、135°=-0.71、180°=-1というように、90°の0を境に1から-1の間の値を取ります。
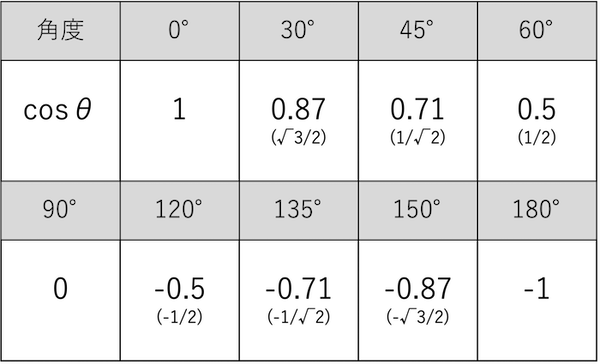 相関係数は1に近いと正の相関が強く、0が相関なし、-1に近いと負の相関が強くなります。この相関係数がcosθの三角比と一致します。
相関係数は1に近いと正の相関が強く、0が相関なし、-1に近いと負の相関が強くなります。この相関係数がcosθの三角比と一致します。
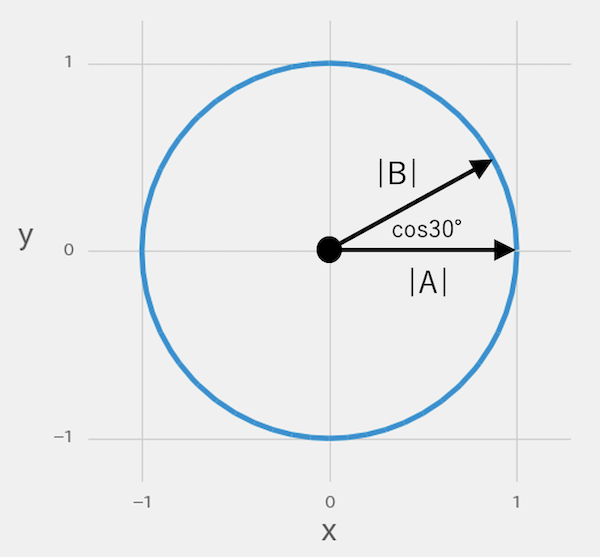 この図の場合、ベクトルAとベクトルBの角度は30°で、cos30°の三角比は0.87です。1に近いため、正の相関があることになります。
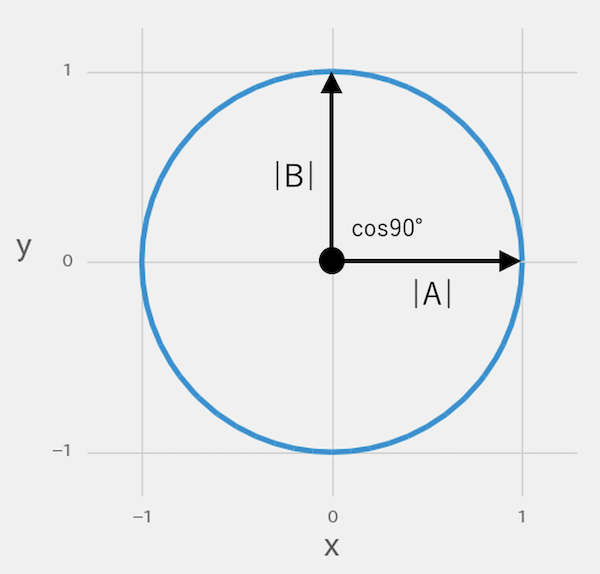
下の図は、ベクトルAとベクトルBが直角です。角度は90°で、cos90°の三角比は0のため、相関がありません。
この図の場合、ベクトルAとベクトルBの角度は30°で、cos30°の三角比は0.87です。1に近いため、正の相関があることになります。
下の図は、ベクトルAとベクトルBが直角です。角度は90°で、cos90°の三角比は0のため、相関がありません。
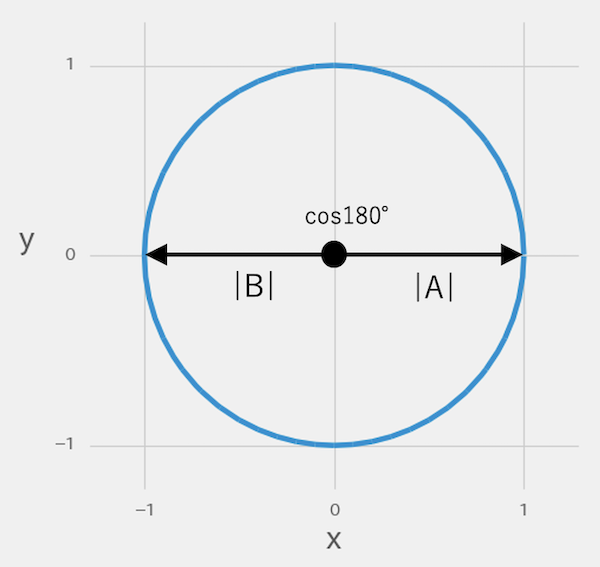
 下の図は、ベクトルAとベクトルBが逆方向を向いています。角度は180°で、cos180°の三角比は-1のため、負の相関です。
下の図は、ベクトルAとベクトルBが逆方向を向いています。角度は180°で、cos180°の三角比は-1のため、負の相関です。
 このように、2つのベクトルの角度が分かると相関が分かります。
cosθは、2つのベクトルの内積と長さ(座標)が分かれば求めることができます。
cosθを使って内積を求める計算方法は以下です。
このように、2つのベクトルの角度が分かると相関が分かります。
cosθは、2つのベクトルの内積と長さ(座標)が分かれば求めることができます。
cosθを使って内積を求める計算方法は以下です。
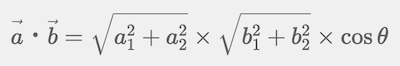 この式を変形して左辺にcosθを持ってくると、次の式になります。
この式を変形して左辺にcosθを持ってくると、次の式になります。
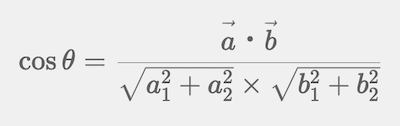 このcosθが、コサイン類似度=相関係数となります。
機械学習の自然言語では、単語や文章をベクトル化して、コサイン類似度を使って相関関係を求めることがあります。
【固有ベクトル・固有値】
ベクトルに行列を掛けて新たなベクトルを作ったとき、変換後のベクトルの向きが、元のベクトルと同じ向きになる(もしくは真逆の向きになる)ことがあります。この場合の変換後のベクトルを「固有ベクトル」と言い、元のベクトルと変換後のベクトルの長さの比を「固有値」と言います。
教師なし学習の主成分分析は、複数の次元を扱いやすい次元数に削減することができますが、そこで固有値と固有ベクトルが利用されます。
なお、公式書籍にコサイン類似度と固有値・固有ベクトルに関する説明はありませんが、理解すると線形代数と機械学習の関係を知ることができます。
このcosθが、コサイン類似度=相関係数となります。
機械学習の自然言語では、単語や文章をベクトル化して、コサイン類似度を使って相関関係を求めることがあります。
【固有ベクトル・固有値】
ベクトルに行列を掛けて新たなベクトルを作ったとき、変換後のベクトルの向きが、元のベクトルと同じ向きになる(もしくは真逆の向きになる)ことがあります。この場合の変換後のベクトルを「固有ベクトル」と言い、元のベクトルと変換後のベクトルの長さの比を「固有値」と言います。
教師なし学習の主成分分析は、複数の次元を扱いやすい次元数に削減することができますが、そこで固有値と固有ベクトルが利用されます。
なお、公式書籍にコサイン類似度と固有値・固有ベクトルに関する説明はありませんが、理解すると線形代数と機械学習の関係を知ることができます。




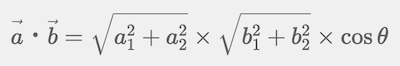 この式を変形して左辺にcosθを持ってくると、次の式になります。
この式を変形して左辺にcosθを持ってくると、次の式になります。
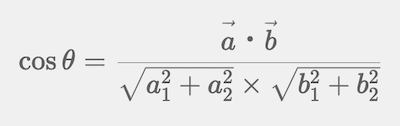 このcosθが、コサイン類似度=相関係数となります。
機械学習の自然言語では、単語や文章をベクトル化して、コサイン類似度を使って相関関係を求めることがあります。
【固有ベクトル・固有値】
ベクトルに行列を掛けて新たなベクトルを作ったとき、変換後のベクトルの向きが、元のベクトルと同じ向きになる(もしくは真逆の向きになる)ことがあります。この場合の変換後のベクトルを「固有ベクトル」と言い、元のベクトルと変換後のベクトルの長さの比を「固有値」と言います。
教師なし学習の主成分分析は、複数の次元を扱いやすい次元数に削減することができますが、そこで固有値と固有ベクトルが利用されます。
なお、公式書籍にコサイン類似度と固有値・固有ベクトルに関する説明はありませんが、理解すると線形代数と機械学習の関係を知ることができます。
このcosθが、コサイン類似度=相関係数となります。
機械学習の自然言語では、単語や文章をベクトル化して、コサイン類似度を使って相関関係を求めることがあります。
【固有ベクトル・固有値】
ベクトルに行列を掛けて新たなベクトルを作ったとき、変換後のベクトルの向きが、元のベクトルと同じ向きになる(もしくは真逆の向きになる)ことがあります。この場合の変換後のベクトルを「固有ベクトル」と言い、元のベクトルと変換後のベクトルの長さの比を「固有値」と言います。
教師なし学習の主成分分析は、複数の次元を扱いやすい次元数に削減することができますが、そこで固有値と固有ベクトルが利用されます。
なお、公式書籍にコサイン類似度と固有値・固有ベクトルに関する説明はありませんが、理解すると線形代数と機械学習の関係を知ることができます。