選択肢1が正解です。 左上から右下の対角線のグラフは、各特徴量のヒストグラムです。 他の選択肢は正しい説明です。 次の図は、matplotlibを拡張したライブラリ「seaborn」で、irisのデータを可視化したものです。配色などは変わりますが、scatter_matrix関数でも同様の図になります。 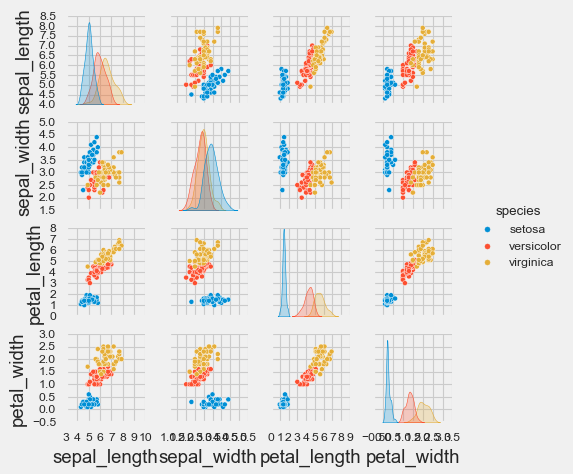irisのデータは、3種類の花を4つの特徴量で表しています。 3種類の花は、図の青色、緑色、橙色で色分けされています。 また、次の4つの特徴量が、y軸は上から下へ、x軸は左から右へ並んでいます。 sepal_length（がく片の長さ） sepal_width（がく片の幅） petal_length（花びらの長さ） petal_width（花びらの幅） 左上から右下の対角線は同じ特徴量が交差しているため、散布図ではなく各特徴量のヒストグラムが表示されます。 対角線以外は、x軸とy軸の2つの特徴量が散布図で表示されます。 例えば、右下にある「petal_length（花びらの長さ）」と「petal_width（花びらの幅）」は、右上がりの直線の周辺に分布しているため、正の相関が強いと言えます。花びらの長さが長くなるにつれ、花びらの幅が広くなります。 他の特徴量も全体的には右上がりに分布しているため、正の相関があると言えそうです。また、3種類の花の色も集中しているため、分類しやすいデータと言えます。 このように、scatter_matrix関数で可視化するだけで、データの傾向が分かることがあります。 （公式書籍 p.175-176）