データ分析・上級問題チェック
問題 8 /40
指数とシグモイド関数に関する説明で、誤っているものはどれか。なお、「^」は指数を表す記号とする。
選択 1
「y=2^x」は指数関数である。
選択 2
「2^-2」は1である。
選択 3
シグモイド関数の出力結果は0と1の間になる。
選択 4
シグモイド関数のグラフは、x=0、y=0.5の点対称グラフである。
解説
選択肢2が正解です。
【選択肢1】
「y=2^x」は指数関数である。
正しい説明です。
この「y=2のx乗」でxを0から順に大きくすると、yは次の値になります。
x=0 → y=1
x=1 → y=2
x=2 → y=4
x=3 → y=8
x=10 → y=1024
x=20 → y=1048576
最初は緩やかに増加しますが、xの値が大きくなるとyの値が急激に大きくなります。これが比喩的に使われる「指数関数的に増加する」の意味となります。
なお、「y=x^2」は指数関数ではなく2次関数です。
【選択肢2】
「2^-2」は1である。
誤った説明です。
「2の-2乗」は0.25(4分の1)となります。
マイナスの指数は、最初に指数のマイナスを無視して計算します。2の-2乗の場合、2を2乗して4になります。その数字を分母に置き、分子に1を置くとマイナスの指数の計算結果になります。
以下のシグモイド関数の分母にあるeの-x乗も、同様の計算で求めます。
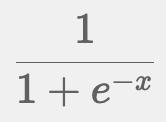 【選択肢3】
シグモイド関数の出力結果は0と1の間になる。
正しい説明です。
シグモイド関数の出力は、xが大きくなるにつれて1に近づき、小さくなるにつれて0に近づきます。シグモイド関数のグラフは以下です。
【選択肢3】
シグモイド関数の出力結果は0と1の間になる。
正しい説明です。
シグモイド関数の出力は、xが大きくなるにつれて1に近づき、小さくなるにつれて0に近づきます。シグモイド関数のグラフは以下です。
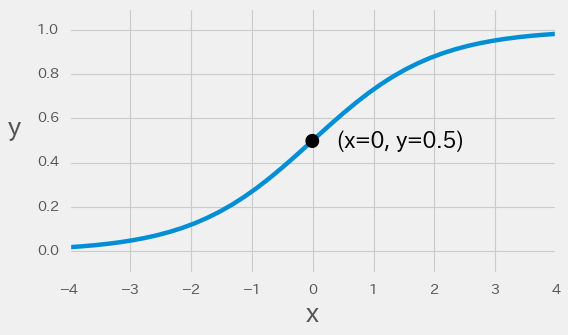 シグモイド関数の分母に登場するeはネイピア数です。ネイピア数を2.17とした場合の出力は以下となります。
x=-5 → y=0.02...
x=-3 → y=0.08...
x=-1 → y=0.31...
x=0 → y=0.5
x=1 → y=0.68...
x=3 → y=0.91...
x=5 → y=0.97...
xの値をどれだけ大きくしても、出力が0と1の間に収まります。この性質は、教師あり学習の分類のロジスティック回帰で利用されています。出力が0.5より小さい場合はAに分類し、0.5より大きい場合はBに分類するというような使い方です。
【選択肢4】
シグモイド関数のグラフは、x=0、y=0.5の点対称グラフである。
正しい説明です。
シグモイド関数はx=0のときy=0.5となり、グラフはその点を対称とした点対称になります。
(公式書籍 p.56-57)
シグモイド関数の分母に登場するeはネイピア数です。ネイピア数を2.17とした場合の出力は以下となります。
x=-5 → y=0.02...
x=-3 → y=0.08...
x=-1 → y=0.31...
x=0 → y=0.5
x=1 → y=0.68...
x=3 → y=0.91...
x=5 → y=0.97...
xの値をどれだけ大きくしても、出力が0と1の間に収まります。この性質は、教師あり学習の分類のロジスティック回帰で利用されています。出力が0.5より小さい場合はAに分類し、0.5より大きい場合はBに分類するというような使い方です。
【選択肢4】
シグモイド関数のグラフは、x=0、y=0.5の点対称グラフである。
正しい説明です。
シグモイド関数はx=0のときy=0.5となり、グラフはその点を対称とした点対称になります。
(公式書籍 p.56-57)
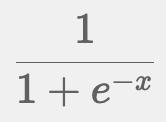 【選択肢3】
シグモイド関数の出力結果は0と1の間になる。
正しい説明です。
シグモイド関数の出力は、xが大きくなるにつれて1に近づき、小さくなるにつれて0に近づきます。シグモイド関数のグラフは以下です。
【選択肢3】
シグモイド関数の出力結果は0と1の間になる。
正しい説明です。
シグモイド関数の出力は、xが大きくなるにつれて1に近づき、小さくなるにつれて0に近づきます。シグモイド関数のグラフは以下です。
