データ分析・上級問題チェック
問題 9 /40
ベクトルの内積に関する説明で、誤っているものはどれか。
選択 1
ベクトルの内積は、結果がベクトルではなくスカラーで返る。
選択 2
座標(a1, a2)と(b1, b2)のベクトルの内積は、次の計算式で求めることができる。
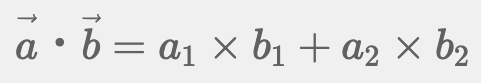
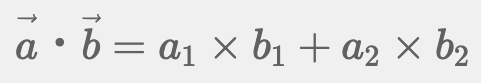
選択 3
座標(a1, a2)と(b1, b2)のベクトルの内積は、次の計算式で求めることができる。
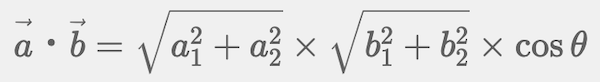
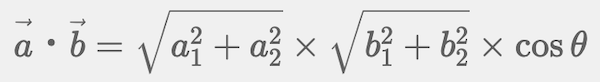
選択 4
内積が0の場合、2つのベクトルは正反対の方向を向いている。
解説
選択肢4が正解です。
内積が0の場合、2つのベクトルは正反対ではなく直角に交わっています。
ベクトルの内積は、結果がベクトルではなく数値(スカラー)で返ります。この数値は、2つのベクトルで作る「平行四辺形の面積」と考えると分かりやすいです。
内積の計算方法は選択肢2と3の方法があり、どちらも同じ結果になります。
【選択肢2】
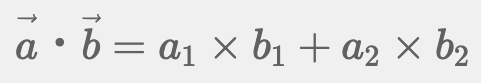 各ベクトルの成分を掛けて足す計算方法です。下図のように座標(2,0)と(1,1)であれば、「(2×1) + (0×1) = 2」が内積となります。
各ベクトルの成分を掛けて足す計算方法です。下図のように座標(2,0)と(1,1)であれば、「(2×1) + (0×1) = 2」が内積となります。
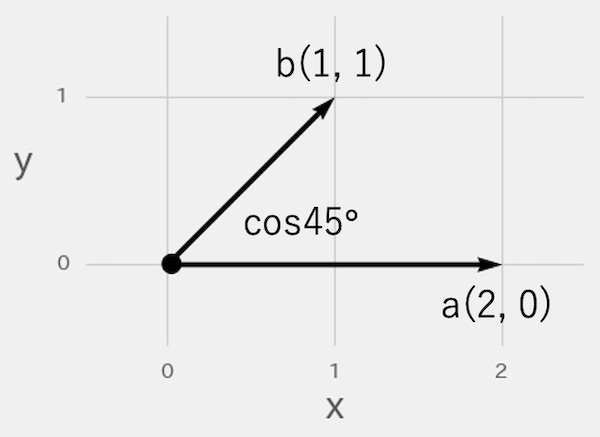 【選択肢3】
【選択肢3】
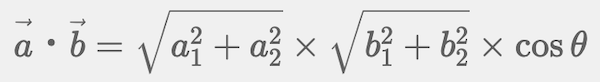 cosθを使う計算方法です。各ベクトルの長さを三平方の定理で計算し、それぞれを掛けて、cosθの三角比を掛けます。上図のようにcos45°(1/√2)であれば、「√(4+0) × √(1+1) x (1/√2) = 2」が内積となります。
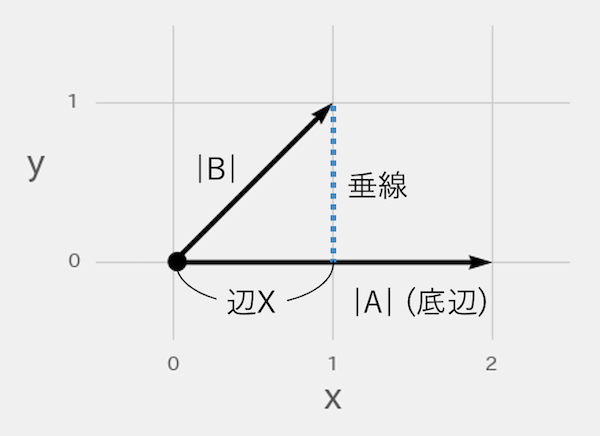
面積の公式は「底辺×高さ」です。内積を「平行四辺形の面積」と考える場合、底辺はベクトルAの長さで、高さはベクトルBからベクトルAに下ろした垂線の長さです。
この垂線は、次の図の辺Xと同じ長さになります。辺XはベクトルBの真上から光を当てたときの影になるため、「ベクトルBの正射影」と呼びます。
cosθを使う計算方法です。各ベクトルの長さを三平方の定理で計算し、それぞれを掛けて、cosθの三角比を掛けます。上図のようにcos45°(1/√2)であれば、「√(4+0) × √(1+1) x (1/√2) = 2」が内積となります。
面積の公式は「底辺×高さ」です。内積を「平行四辺形の面積」と考える場合、底辺はベクトルAの長さで、高さはベクトルBからベクトルAに下ろした垂線の長さです。
この垂線は、次の図の辺Xと同じ長さになります。辺XはベクトルBの真上から光を当てたときの影になるため、「ベクトルBの正射影」と呼びます。
 この正射影の長さは「ベクトルB × cosθ」と一致します。この式は、内積を求める「ベクトルA × ベクトルB × cosθ」の後半の式と同じです。つまり内積は、「ベクトルA × 正射影の長さ(=垂線)」と置き換えることができます。
この正射影の長さは「ベクトルB × cosθ」と一致します。この式は、内積を求める「ベクトルA × ベクトルB × cosθ」の後半の式と同じです。つまり内積は、「ベクトルA × 正射影の長さ(=垂線)」と置き換えることができます。
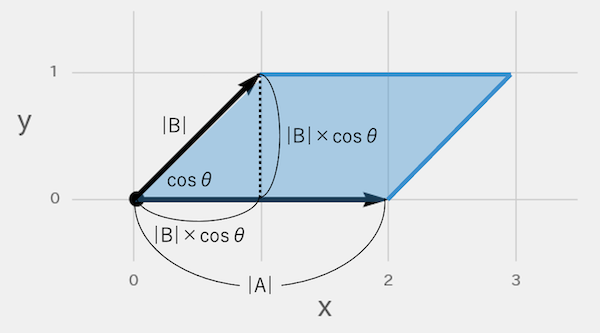 こうして内積は、「底辺(ベクトルA) × 高さ(正射影=垂線)」で求める面積と考えることができます。
こうして内積は、「底辺(ベクトルA) × 高さ(正射影=垂線)」で求める面積と考えることができます。
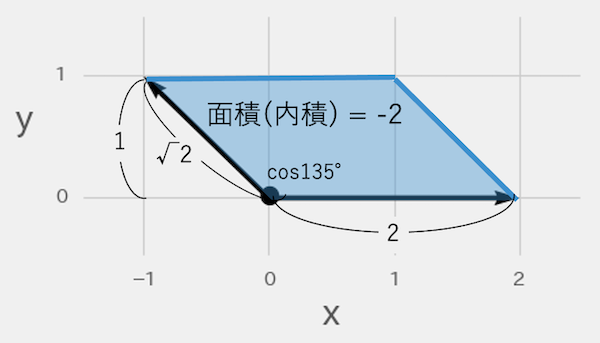
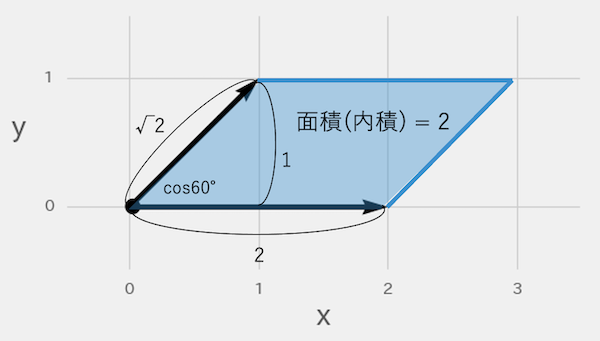 cosθが135°のように鈍角になっている場合は、次の図のような面積になります。cos135°が「-1/√2」のため、面積も内積も-2になります。通常、面積は正の値になりますが、内積として考える場合は負の値も持ちます。
cosθが135°のように鈍角になっている場合は、次の図のような面積になります。cos135°が「-1/√2」のため、面積も内積も-2になります。通常、面積は正の値になりますが、内積として考える場合は負の値も持ちます。
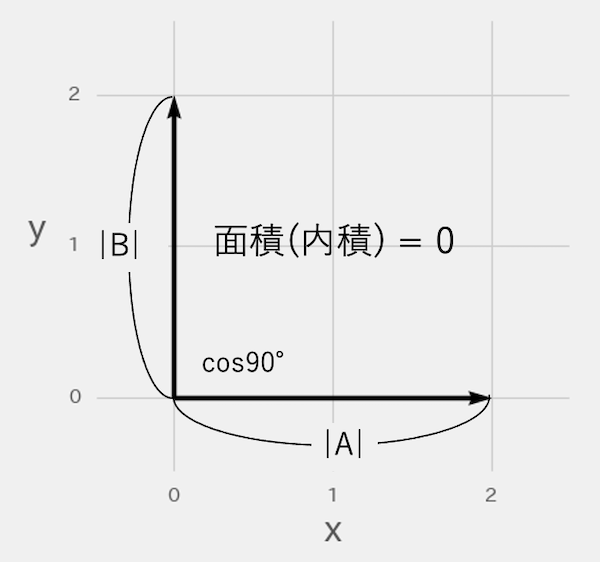
 ベクトルAとベクトルBが直角に交わるときも、面積で考えることができます。面積を求めるときの高さは、BベクトルではなくBベクトルの正射影です。Bベクトルに真上から光を当てると、影ができないため長さは0になります。「長さ0 × 底辺 = 0」のため面積は0になり、内積もcos90°の三角比が0のため0になります。
ベクトルAとベクトルBが直角に交わるときも、面積で考えることができます。面積を求めるときの高さは、BベクトルではなくBベクトルの正射影です。Bベクトルに真上から光を当てると、影ができないため長さは0になります。「長さ0 × 底辺 = 0」のため面積は0になり、内積もcos90°の三角比が0のため0になります。
 なお、2つのベクトルが正反対を向いている場合はcos180°のため三角比が-1、全く同じ方向を向いている場合はcos0°のため三角比が1になります。
ベクトルの内積は機械学習でも利用されます。個々のデータをベクトルととらえ、内積の正負や大きさに応じてデータを分類することがあります。
(公式書籍 p.65)
なお、2つのベクトルが正反対を向いている場合はcos180°のため三角比が-1、全く同じ方向を向いている場合はcos0°のため三角比が1になります。
ベクトルの内積は機械学習でも利用されます。個々のデータをベクトルととらえ、内積の正負や大きさに応じてデータを分類することがあります。
(公式書籍 p.65)
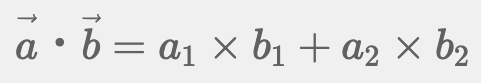 各ベクトルの成分を掛けて足す計算方法です。下図のように座標(2,0)と(1,1)であれば、「(2×1) + (0×1) = 2」が内積となります。
各ベクトルの成分を掛けて足す計算方法です。下図のように座標(2,0)と(1,1)であれば、「(2×1) + (0×1) = 2」が内積となります。
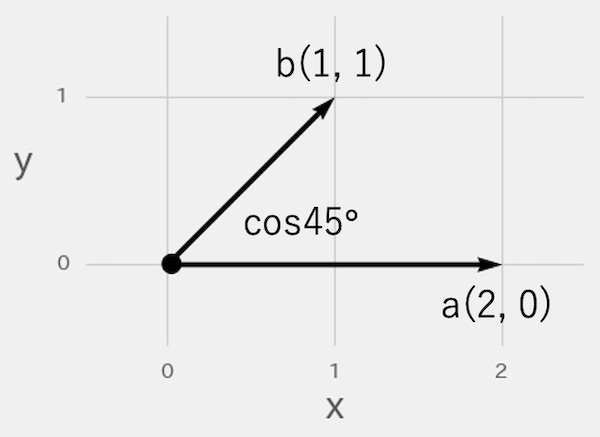
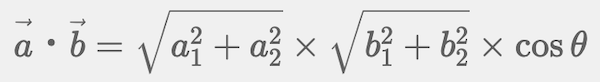 cosθを使う計算方法です。各ベクトルの長さを三平方の定理で計算し、それぞれを掛けて、cosθの三角比を掛けます。上図のようにcos45°(1/√2)であれば、「√(4+0) × √(1+1) x (1/√2) = 2」が内積となります。
面積の公式は「底辺×高さ」です。内積を「平行四辺形の面積」と考える場合、底辺はベクトルAの長さで、高さはベクトルBからベクトルAに下ろした垂線の長さです。
この垂線は、次の図の辺Xと同じ長さになります。辺XはベクトルBの真上から光を当てたときの影になるため、「ベクトルBの正射影」と呼びます。
cosθを使う計算方法です。各ベクトルの長さを三平方の定理で計算し、それぞれを掛けて、cosθの三角比を掛けます。上図のようにcos45°(1/√2)であれば、「√(4+0) × √(1+1) x (1/√2) = 2」が内積となります。
面積の公式は「底辺×高さ」です。内積を「平行四辺形の面積」と考える場合、底辺はベクトルAの長さで、高さはベクトルBからベクトルAに下ろした垂線の長さです。
この垂線は、次の図の辺Xと同じ長さになります。辺XはベクトルBの真上から光を当てたときの影になるため、「ベクトルBの正射影」と呼びます。




